Application of calculated matched filter
![]()
![]()
What is a Matched Filter?
A matched filter is a processing operator designed to maximize the Signal-to-Noise Ratio (SNR) of a known seismic wavelet. It is the optimal filter (in the least-squares sense) for detecting or enhancing a signal whose shape is known or estimated.
A matched filter is the time-reversed version of the desired signal (wavelet) used as a convolution operator to enhance that signal in the noisy trace.
How Does a Matched Filter Work?
The matched filter works by cross correlating the seismic trace with a reference wavelet: y(t) = x(t) * w(-t)
Where:
•x(t) = recorded seismic trace
•w(t) = known or estimated wavelet
•w(-t) = time-reversed wavelet (the matched filter)
•* = convolution
•If the wavelet in the recorded data matches the reference wavelet in the filter constructive interference, SNR increases.
•If the noise is random, it does not correlate which means suppressed.
This is why matched filtering is widely used after correlation, deconvolution, or vibrator processing.
Where is Matched Filtering used?
•Vibroseis processing (matching pilot sweep to correlated data)
•Post-stack enhancement (boosting a specific reflection event)
•Target detection
•Deconvolution & wavelet shaping
Mathematical Basis of Matched filter design and application
1. Filter Design
Given a reference wavelet w(t), the matched filter h(t) is: h(t) = w(-t) i.e., reverse the wavelet in time.
If designing in frequency domain: H(f) = W*(f) Where W*(f) = complex conjugate of the wavelet spectrum.
2. Applying the Filter
Filtered trace = convolution of seismic trace with matched filter: y(t) = x(t) * h(t)
Or equivalently, cross-correlation: Y(t) = x(t) . w(t)
Estimation of the Filter and application on seismic data
Step 1 — Estimate or choose the wavelet
Sources:
•Pilot sweep (Vibroseis)
•Statistical wavelet extraction
•Near-offset wavelet analysis or Near Field Hydrophone
•Well tie wavelet
Step 2 — Create the Matched Filter
Time domain
Wavelet = [w1, w2, w3, ... wn]
Matched filter = [wn, ..., w3, w2, w1] - Reverse the wavelet:
Frequency domain
Take FFT of the wavelet and use its complex conjugate.
Step 3 — Apply to seismic data
Use convolution: Y(t) = X(t) * H(t)
Or in frequency domain: Y(f) = X(f) . H(f)
![]()
![]()
Input DataItem
Input gather - connect/reference to the data that needs to be matched with the Template/Desired gather.
Filter - connect/reference to the Filter generated by the Match filter - Calculate module. This filter operator is used to match the Input gather with Template gather.
![]()
![]()
There are no parameters required for this module so the user can ignore it.
![]()
![]()
Auto-connection - By default, TRUE(Checked).It will automatically connects to the next module. To avoid auto-connect, the user should uncheck this option.
Number of threads - One less than total no of nodes/threads to execute a job in multi-thread mode. Limit number of threads on main machine.
Skip - By default, FALSE(Unchecked). This option helps to bypass the module from the workflow.
![]()
![]()
Output DataItem
Output gather - outputs the matched gather
There is no information available for this module so the user can ignore it.
![]()
![]()
In this example workflow, we are applying previously calculated Filter operator to the Input/target gather to match with the Template/source/desired gather. Since, it requires only the input gather that needs to be matched with Template gather, it doesn't require any parameters. All the user must make the Filter operator reference.
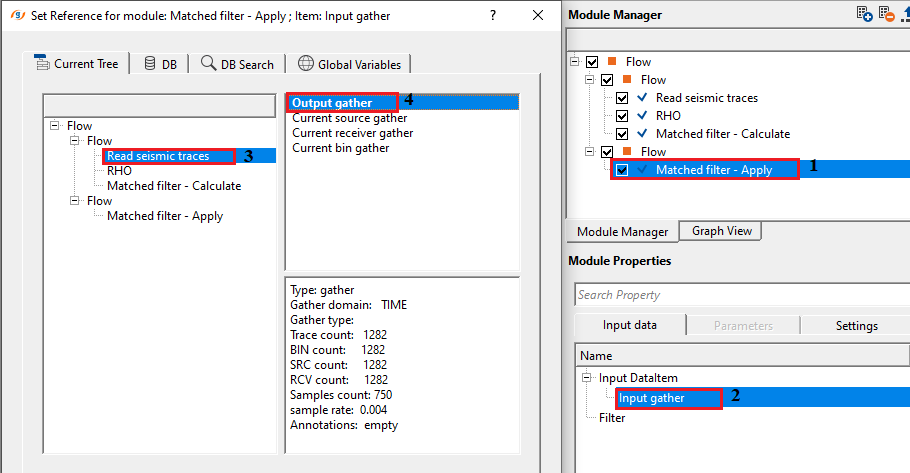
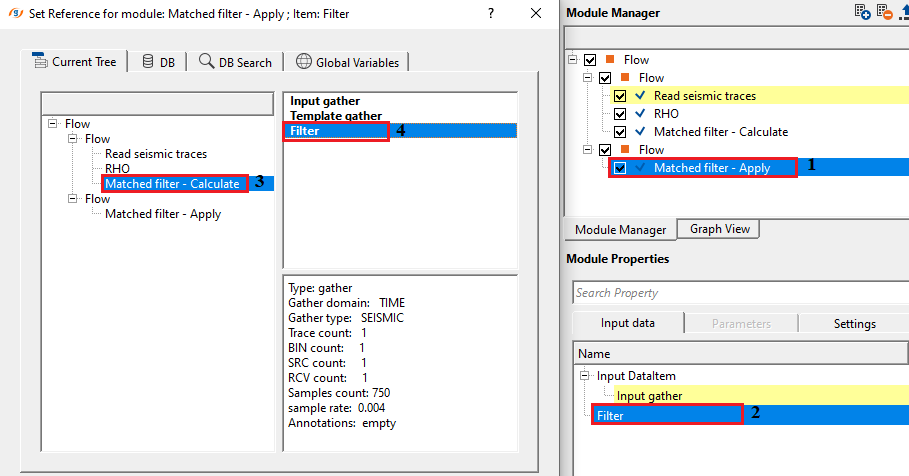
Execute the module and generate the vista items.
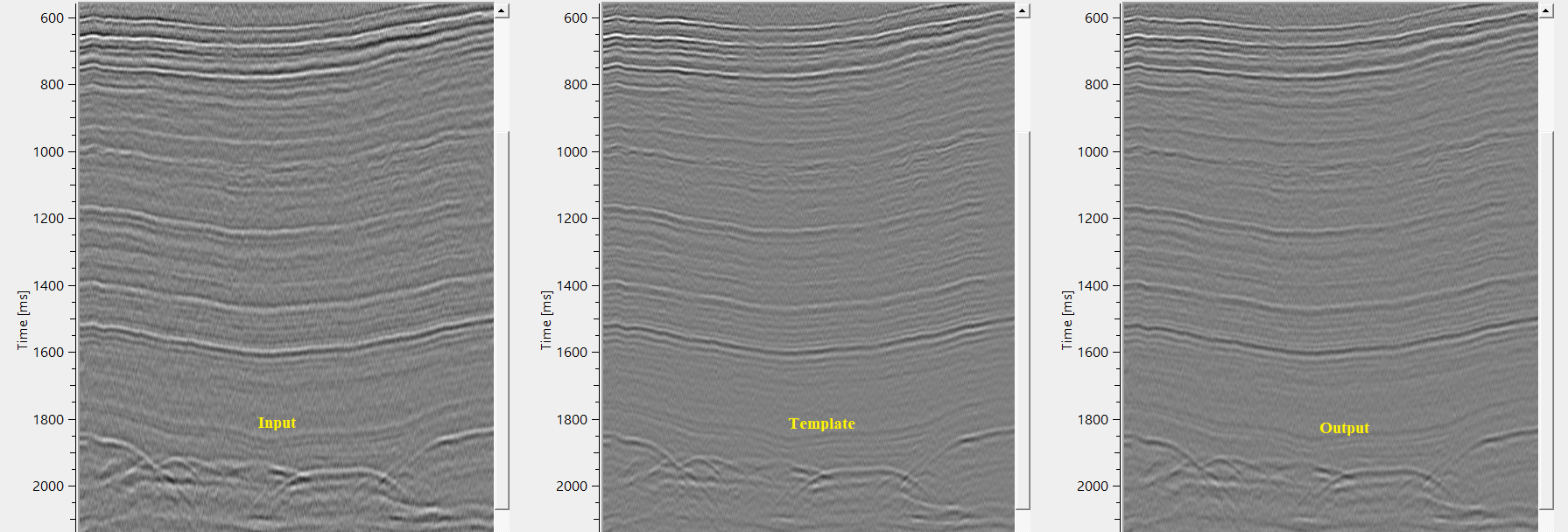
In the above image, we matched the input gather (1st) with Template gather (2nd) by designing a Filter operator. Final output gather (3rd) is matching with the Template gather (2nd).
![]()
![]()
There are no action items available for this module.
![]()
![]()
YouTube video lesson, click here to open [VIDEO IN PROCESS...]
![]()
![]()
Yilmaz. O., 1987, Seismic data processing: Society of Exploration Geophysicist
 * * * If you have any questions, please send an e-mail to: support@geomage.com * * *
* * * If you have any questions, please send an e-mail to: support@geomage.com * * *