Static calculation by using tomography 2D algorithm
![]()
![]()
Tomography plays a key role in seismic imaging. Be it is a building depth velocity model or calculating the refraction statics by generating the near surface model. Refraction Tomography statics are used in the event of regular refraction statics are not giving optimum results or to improve the refraction statics solution. In this method, the weathering zone (WZ) is parametrized as a number of cells that used for filling up a depth velocity model. Travel times are goes through the cell-model, and residuals times are converted into velocity variations in 2D cells. Here we are able to calculate vertical velocity gradient due to the fact that tomography is a nonlinear move out modeling of the first arrivals (Fig. 1).
The tomographic is sensitive to the initial model due to the fact that the nonlinear solution performs by iterating the ray tracing and velocity is updated by local linearization, so the solution of tomography is depending on quality of first breaks picking. Therefore, if we have 2D data set it is more reasonable to make FB picking more accurate by doing it manually.
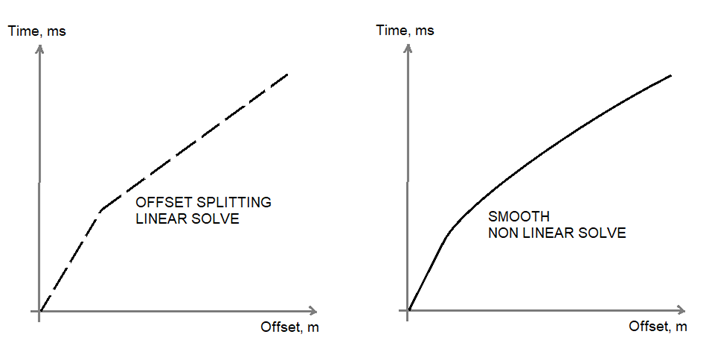
Fig. 1 Linear (left) and nonlinear (right) solutions comparison.
Tomo statics 2D module requires the first break picks. In this module, it start with an initial model and starts updating the model during each iteration until it converges to the best solution (Fig.3).
The tomo-statics modules in the g-Platform system are based on the Fresnel seismic travel time tomography. A Fresnel volume approach is applied to represent wave propagation for seismic travel time tomography instead of rays. A Fresnel volume is defined as a set of many waves delayed after the shortest travel time by less than half a period. It is derived by calculating travel times both from a source and from a receiver. Tracing rays from sources to receivers is completely avoided.This considerably reduces computational time. We solved the eikonal equation by using a finite-difference method to calculate travel times. The advantage of this approach is as follows: first, the frequency of wave can be introduced into analysis. Therefore, we can evaluate the resolution of seismic tomography. Next, the smoothing feature can be naturally introduced. Finally, Fresnel volumes with finite bandwidth considerably reduces the sparseness of ray distribution.
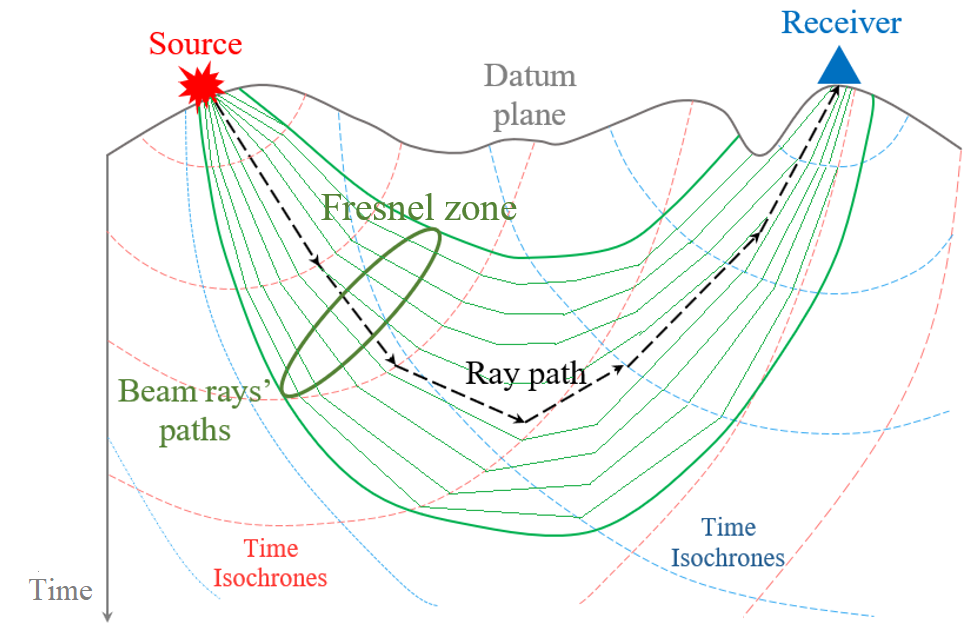
Fig. 2. Travel times scheme.
The more physically-realistic representation of wave propagation is to treat a ray path as a beam with finite width. Using a Fresnel volume is a natural and an effective approach. A Fresnel volume is a set of many rays delayed after the shortest travel time by less than half the period of wave. The rays in a Fresnel volume are added constructively to form the first-arrival of wave. There have been several studies on the application of Fresnel volumes to seismic tomography since Harlan(1990). In this study, first, we discussed the characteristics of Fresnel volumes. Next, we formulated the inversion procedure. Then, we investigated the resolution of tomography with respect to the frequency (Toshiki W. Seismic travel time tomography using Fresnel volume approach).
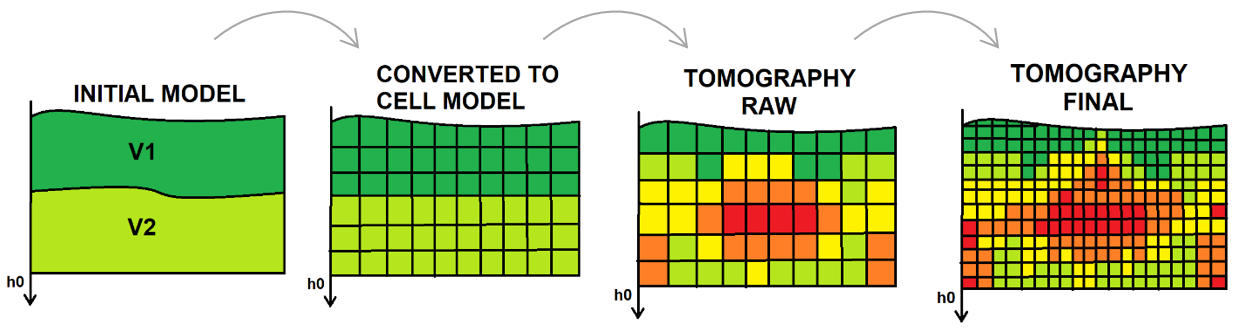
Fig. 3 Tomography steps.
Usually, testing parameters starts with wider cells size of the model because the main goal is to find the more appropriate values for other parameters. When we have optimal result, it is reasonable to reduce cell size and increase the number of iterations. Eventually, a dense gradient depth velocity model is calculated as well as statics for source and receiver. A depth velocity model we can use in the depth migration step as the upper part of the PSDM model.
![]()
![]()
Solve - launch tomography calculations.
Import FB picking - import first breaks from files. Formats: Binary, ASCII. provide the first break picks to compute the tomography statics.
Click on Import FBPicking from the action item menu and provide the first break picks to compute the tomography statics. The user can define the parameters like number of velocity updates, regression aperture etc. and try to execute the module. To visualize the tomography velocity model and convergence, the user should generate the vista items. Following are the displays from the Vista Groups.
![]()
![]()
Output geometry - definition for the output geometry parameters of the resulting velocity model.
Input trace headers - input trace headers.
Input SEG-Y data handle - input seismic traces (samples).
![]()
![]()
Definition cell-velocity model.
Deepest refractor velocity - the maximum values of guide-wave.
Datum – start value for tomography calculation, constant datum.
Max depth – maximum depth in meters of the model.
Step Z depth out – vertical cell size in meters.
Step X depth out – horizontal cell size in meters.
Step depth time table – vertical step for travel time solution, smaller value – more detailed result, but time consuming.
Horizontal smooth – horizontal velocity smoothing in meters.
Frequency- Parameter for making solution more detailed in terms of travel time decomposition, bigger value – more detailed result (high spatial frequency), but time consuming. Pay attention on figure 3 Travel times scheme, green constrain depend on this parameter, less frequency - smoothie result.
Tomography iterations.
Allows to have velocity inversion on the model.
Options for interpolation missing first breaks picks:
Nearest – get picks from the nearest traces, use it in case of small gaps in FB picks.
Regression – model picks by using regression method.
Value for making minimum velocity constrain (m/s).
Value for making maximum velocity constrain (m/s).
Value for making minimum offset constrain (m).
Value for making maximum offset constrain (m).
Step for splitting offset by classes (m).
Value of aperture for regression algorithm (m), bigger value – smoother solution.
Maximum deviation (picking to model)
Maximum variations of observed picks according into the model trend.
Visual parameters for displaying velocity model, it is not used for calculations:
Values above the relief elevations for filling.
Velocity filling – define exact value for filling.
Samples topo fill – how many samples to fill.
Residual statics solver parameters:
Step X depth time for solver - Vertical step for residual travel time solution, smaller value – more detailed result, but time consuming.
Regression aperture residual - Value of aperture for regression algorithm (m), bigger value – smoother solution.
Max pick time deviation - Maximum picking variations (ms) for residual static solution.
Global iteration count - Number of global iterations for residual static solution.
Local iteration count - Number of local iterations for residual static solution.
![]()
![]()
SegyCacheParams - parameters for caching SEGY file.
Execute on - CPU or GPU processors.
Distribution options:
Parameters for launching a workflow in cluster mode:
Distributed execution - launching a workflow in cluster mode.
Bulk size - chunk size for calculation on one node.
Number of threads - entire number of threads for calculations.
![]()
![]()
Current source gather - source gather with no statics corrections applied.
Current source gather applied - source gather with statics corrections applied.
Current receiver gather - receiver gather with no statics corrections applied.
Current receiver gather applied - receiver gather with statics corrections applied.
Current bin gather - bin gather with no statics corrections applied.
Current bin gather applied - bin gather with statics corrections applied.
Calculated refraction velocity - velocity model.
Statics correction item - static corrections.
![]()
![]()
For the example workflow, we use a vibroseis seismic acquisition Poland 2D line that is accessible on the internet free or it is also included to the g-Platform installation (C:\Program Files (x86)\Geomage\gPlatform\demodata\Poland_2D_Vibroseis_LINE_01). Demo data also consists of the FB picking file on your disk in the same folder with the input seismic data set, but you just need to convert ASCII FB pick file into Binary one via Refraction FB picking - azimuthal solver guide / phase / aperture module (import->export). So, we can use the module Tomo statics 2D which requires first breaks as mandatory input data set. Connect all input data vectors from the previous module of DB:

Fig. 4. Tomo statics 2D input parameters.
Usually, testing parameters starts with wider cells size of the model because initially the main goal is to find the most appropriate values for other parameters. When we have optimal result, it is reasonable to reduce cell size and increase the number of iterations. Eventually, a dense gradient depth velocity model is calculated as well as static corrections (ms) for sources and receivers. A depth velocity model may be used for the depth migration step as the upper part of the PSDM model.

Fig. 5. Tomography parameters.
Now we have defined all the parametrization and the next step is launching the tomography calculation by double LMB click on the module or pressing Solve action. To visualize the tomography velocity model and convergence, the user should generate the vista items. The module generates many QC windows: the location map, convergence refraction tomo, tomography velocity view and Current source/receiver/bin gather.
For tomography velocity view, the user can define how many number of iteration required in the parameters tab. Once the solution is computed we can QC the statics result by going to the any one of the current source/receiver/bin gather and enable/disable the Current source gather and Current source gather applied options from the View properties of the Current source/receiver/bin gather. Interactive fast QC by applying statics correction on gathers with different sorting: source, receiver and bin.
Check the source gather before and after statics applying. Choose by LMB clicking on any source on the location map:
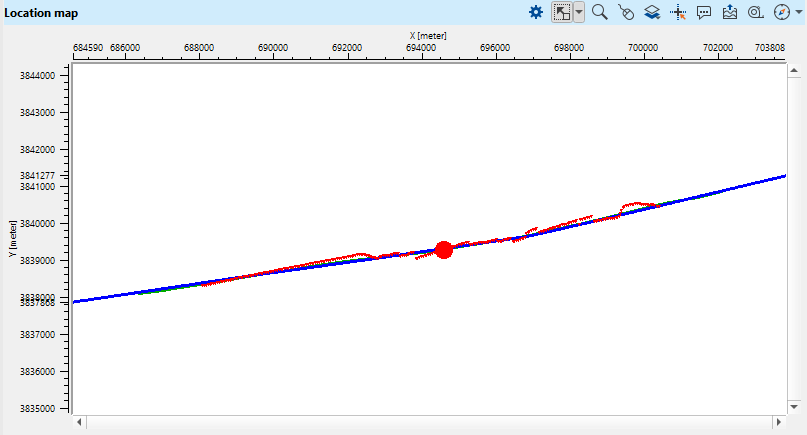
Fig. 6. Source (red) and receiver (blue) interactive map.
And look at the source gather ViewVista window and check gather before and after statics applying:
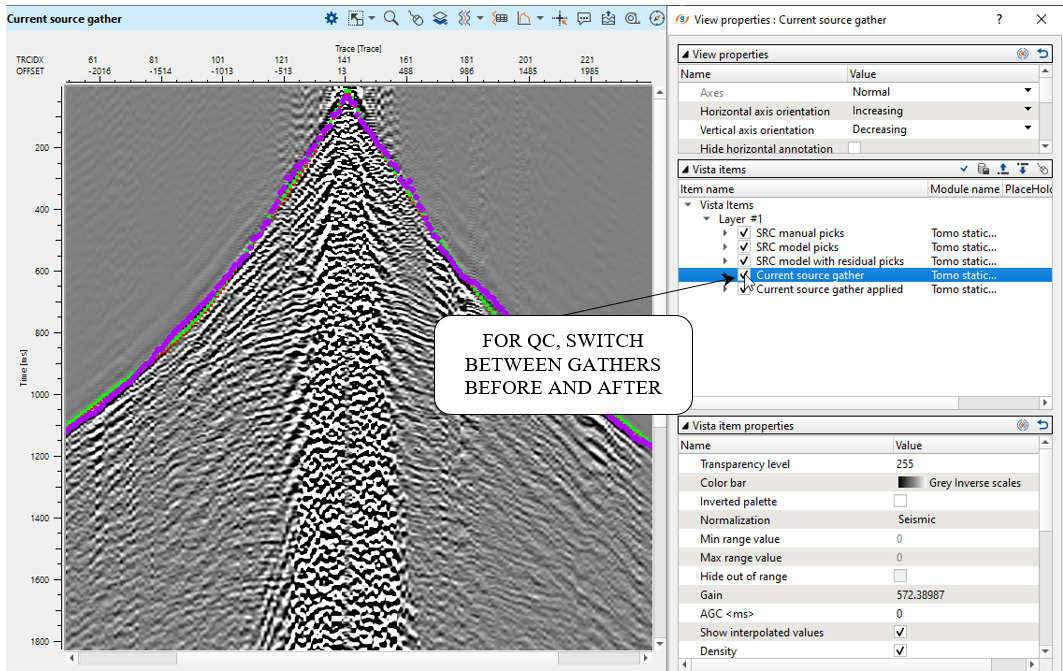
Fig. 7. QC of the resulting statics corrections.
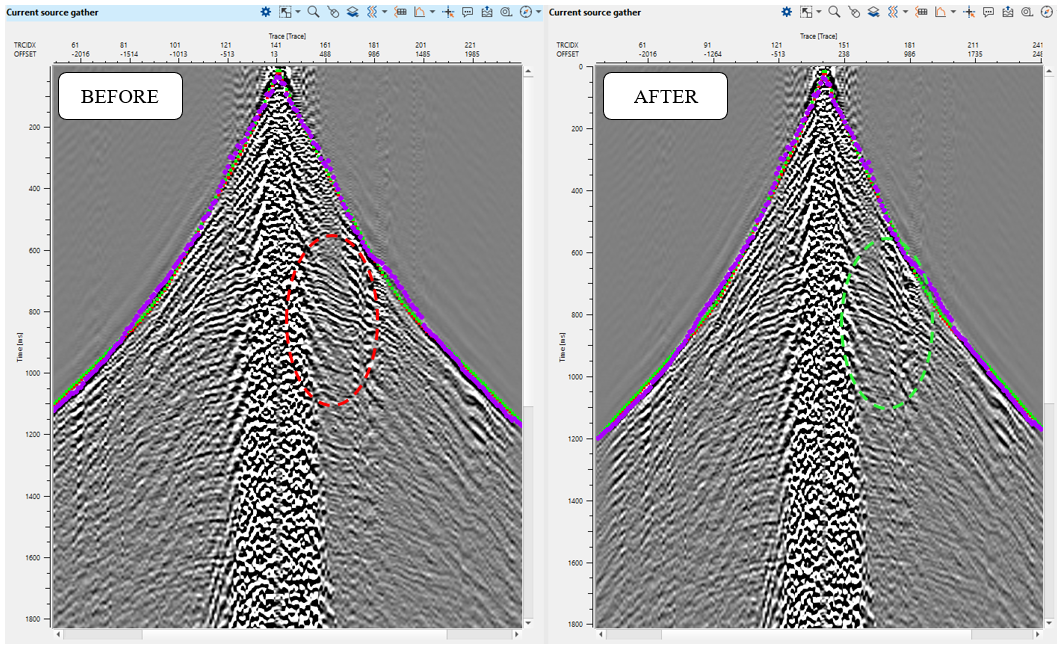
Fig. 8. Source gather before (left) and after (right) tomography statics applying.
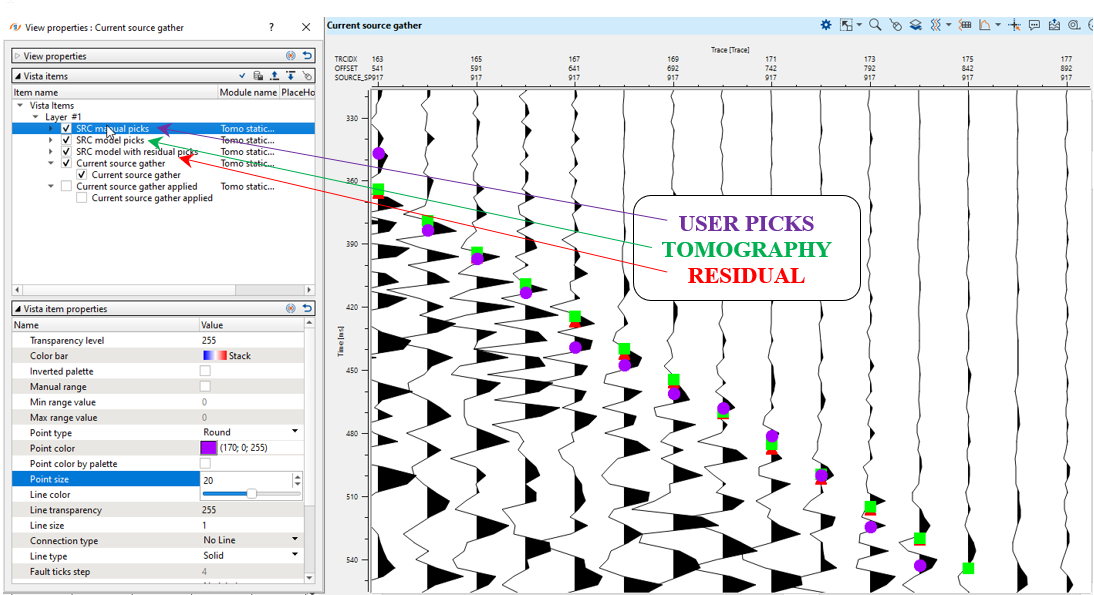
Fig. 9. Source gather and different types of picks for QC: User picks (purple), tomography (green) and residual (red).
Another important QC tool is convergence graphs where you can understand how many tomography iterations should be enough. Every iteration must reduce an error/mistie between observed and modeled times. If the error is too high or the tomo convergence is not matching with the residual convergence then the user can adjust the solver parameters and/or other parameters and click on the Solve option from the action item menu. It will recalculate the solution and update the displays.
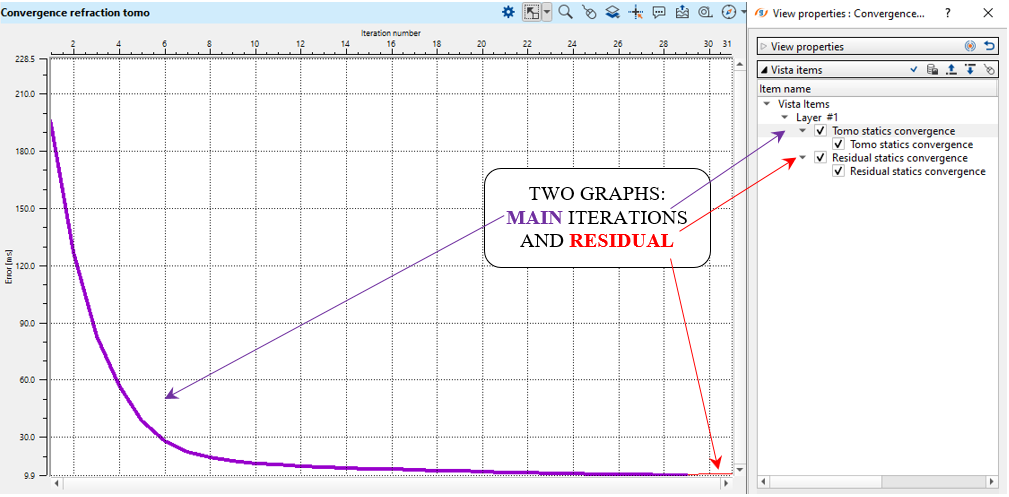
Fig. 10. Graphs of the main-tomography iteration (purple) and residual (red) solution.
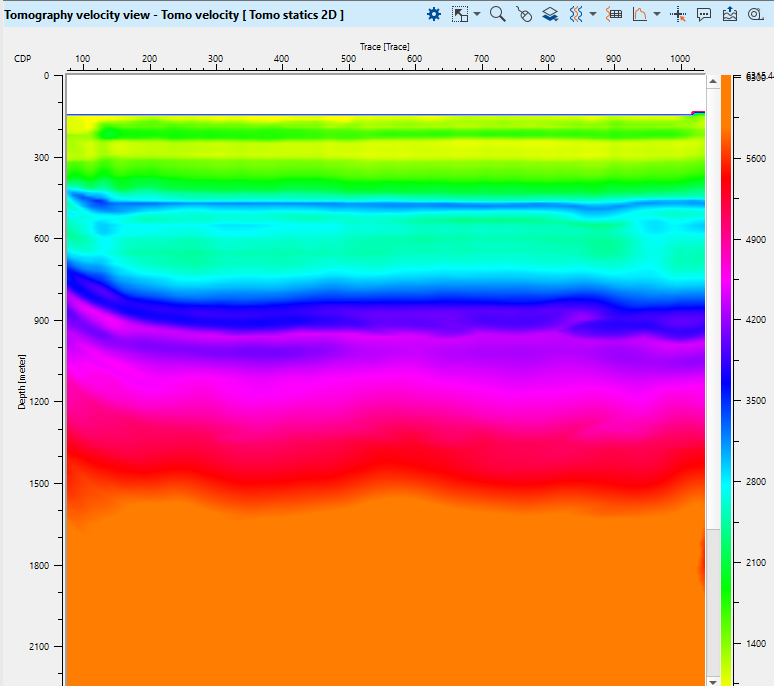
Fig. 11. Depth velocity model after tomography.
![]()
![]()
YouTube video lesson, click here to open [VIDEO IN PROCESS...]
![]()
![]()
Toshiki W. Seismic travel time tomography using Fresnel volume approach, 1999 SEG Technical Program Expanded Abstracts.
Cerveny, V. and Soares, J. E. P., 1992, Fresnel volume ray tracing, Geophysics.
Harlan, W. S., 1990, Tomographic estimation of shear velocities from shallow cross-well seismic data.
Luo, Y. and Schuster, G., 1991, Wave-equation travel time inversion, Geophysics.
Matsuoka,T. and Ezaka, T., 1992,Ray-tracing using reciprocity, Geophysics.
 If you have any questions, please send an e-mail to: support@geomage.com
If you have any questions, please send an e-mail to: support@geomage.com