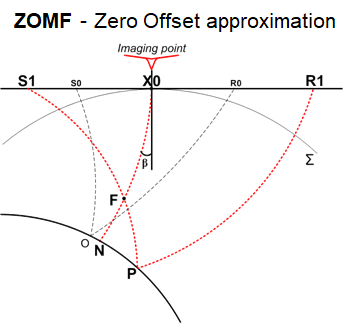
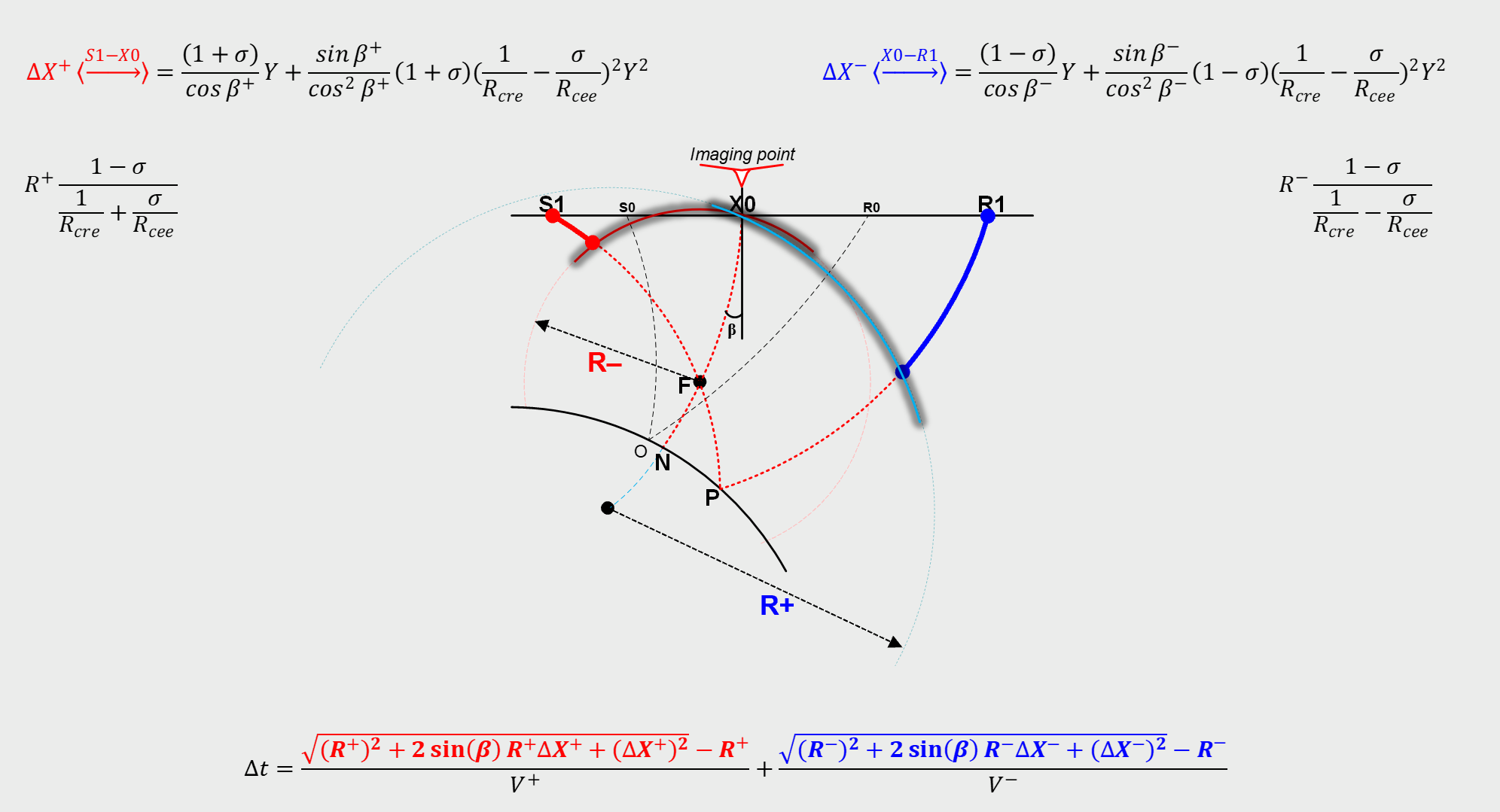
The multifocusing method belongs to the class of methods considers seismic wave front’s propagation and based on the wave kinematics. It has been designed to
approximate the response at the source and receiver points by two spherical waves.
These two spherical waves are mutually related by the focusing quantity. We emphasize the character of the focusing quantity and make clear that it is a parameter function, rather than a parameter itself. The focusing parameter can be designed to be exact in generic cases. Multifocusing opens up a way to search for different geometrical bodies, such as general three dimensional ellipsoids, paraboloids, and an extension of the class of generic cases is certainly feasible.
Also, overburden inhomogeneity and anisotropy (transverse isotropy) may be taken into account. Nevertheless, the multifocusing has the advantage that it applies to
geometries with finite and constant radii of curvature, Rcee, Rcre , and therefore combines generality and simplicity, as well as computational efficiency in the parameter estimation. The multifocusing generic cases and the spherical reflector in particular, allow decomposing a pre-stack seismic data volume into responses from elementary curved reflector segments. They therefore act as templates of seismic reflection response. Even more, it can be shown that the multifocusing is not restricted to reflection response, but applies to the response from strongly curved reflectors as well, and to limiting cases such as point diffractors.